Az alábbi vendégposztot Vásárhelyi Orsolya jegyzi, aki arra vállalkozott, hogy bevezet minket a hálózatok rejtelmes világába, egészen az alapoktól indulva. Az írás egy 4-5 részesre tervezett sorozat kezdete, a fogalmak megalapozása után a további részekben bepillanthatunk majd a hálózatok, a hálózatkutatás mélységeibe és gyakorlati alkalmazásaiba. A szerzőről - aki tagja volt a 2010-es Országos Piackutatási Diákverseny győztes csapatának - további információkat a poszt végén olvashattok.
Nemrég egy nevesebb piackutató cég elemzőjének előadását hallgattuk az egytemen - a téma a piackutatás és a hagyományos módszerek fenntarthatósága volt. A survey statisztika szakos diákokból álló közönséget, nem igazán villanyozták fel a hallottak; gyakorlatilag közölték velünk, hogy feleslegesen strapáljuk magunkat a különböző mintavételi és valószínűségszámítási órákon. Munkát még lehet, hogy találunk, de a kutatási módszerek és eredmények, amiket használni fogunk nem igazán visznek közelebb majd a valósághoz, a tanult módszerek jelentős része már most elavult, az emberek megváltoztak, ismerik a technikáinkat. A jövő a meglévő és megbízható adatok megfelelő elemzésében van, ráadásul etikus módon – hangzott el a ténymegállapítás.
A hálózatkutatás lassan kezd bekerülni a mainstream kutatási módszerek közé és kezdünk ráeszmélni, hogy ez a fiatal tudományág, mennyi különféle szakterületen hasznosítható. Többek között a piackutatásban is. Interneten vásárolunk, telefonálunk, bankkártyával fizetünk, parkolójegyet veszünk, a barátaink képeit kommentáljuk a facebookon, közlekedünk – tehát éljük az életünket, amivel nyomokat hagyunk. Ezek a cselekvések össezfüggnek egymással és más emberek cselekedeteivel, sőt jövőbeli tevékenységeink kb. 80 százalékos pontosággal modellezhetőek ezek alapján. „A hálózatok mindenhol ott vannak”, ahogy Barabási Albert-László, írja Behálózva című könyvében, tehát a marketingkutatásban is. A következő pár cikkben szeretném bemutatni, hogy ez a rengeteg rendelkezésre álló „nyom”, amit puszta modern emberi létezésünkkel gyártunk, hogyan lehet a XXI. századi piackutató hasznára. Ízelítő gyanánt következzen egy kis történeti áttekintés az első gráftól az Internet térképének megrajzolásáig vezető skálafüggetlen hálózatokig - a teljesség igénye nélkül.
Mondhatnám, hogy ez a roppant izgalmas tudomány egyidős az emberiséggel, de ez ebben a formában nem igaz. A hálózatkutatás előfutárának a gráfelméletet tekinthetjük, ami a középiskolában tanult königsbergi (ma Kalinyingrád, Oroszország) hidak problémájával kezdődött 1736-ban. A várost kettészelő Prégel folyón hét híd biztosította az átkelést az egyik oldaláról a másikra és két szigetre (1.ábra). A városlakók kedvelt foglalatossága volt, hogy megpróbáljanak egy olyan útvonalat találni, amivel, miden hídat érintenek, de csak egyszer. Ekkor oldotta meg Leonhard Euler matematikus az unatkozó polgárok kedvenc rejtvényét, az első gráf felrajzolásával. A hídakat egyszerűen a gráf éleinek tekintette, a csomópontok pedig a szárazföldeket jelölték.
Szegény jó porosz kereskedők szomorúan konstatálhatták, hogy kedvenc játékuknak nincs megfejtése. Euler megalkotta a fokszám fogalmát, (ami az egy adott csomópontba becsatlakozó élek számát jelenti) és bebizonyította, hogy csak akkor létezne ebben a gráfban az éleken (hidakon) egyszer végighaladó séta útvonala, ha minden csomópont fokszáma páros lenne.
Az első gráftól azért hosszú út vezetett az Internet térképéig és a hálók marketingcélú használatáig. A XX. századig a hálózatok alatt elsősorban a társadalmi kapcsolatokra épülőkkel foglalkoztak a kutatók, tehát a csomópontok embereket, szervezeteket jelöltek a kapcsolatok pedig a köztük lévő interakciót. (Lehet például rokonszenvi kapcsolat mint a szociometriában.)
A társadalmi hálózatokon kívül, ma már tudjuk „be vagyunk hálózva”, az útvonalaktól, egy cikk tematikus elemzéséig minden értelmezhető hálózatosan. A XX. század közepén két magyar matematikus, nevezetesen Erdős Pál és Rényi Alfréd javasolta (1959), hogy a természettudományos és kommunikációs komplex hálózatok építésénél tekintsék a hálókat véletlenszerűnek. Azaz legyen N számú csomópont, melyek L számú véletlenszerűen elhelyezkedő kapcsolattal rendelkeznek. Ez az egyszerűség és újszerűség felfrissítette a gráfelméletet és beindította a véletlen hálózatokra irányuló kutatásokat. A modell, mivel randomizált, demokratikus, a legtöbb csomópont közel azonos mennyiségű kapcsolattal rendelkezik, így egy valódi véletlen hálózatban a csomópontok fokszámai egy harangalakú (statisztikai tanulmányokból jól ismert) normális eloszlást követnek, tehát jellemezhetőek egy számmal, mint például az átlag.
Ekkoriban jelentek meg a „kisvilág” elméletek, melyek egy 1929-ből származó Karinthy idézettel ragadhatóak meg a legjobban: "Annak bizonyításául, hogy a Földgolyó lakossága sokkal közelebb van egymáshoz, mindenféle tekintetben, mint ahogy valaha is volt, próbát ajánlott fel a társaság egyik tagja. Tessék egy akármilyen meghatározható egyént kijelölni a Föld másfél milliárd lakója közül, bármelyik pontján a Földnek - ő fogadást ajánl, hogy legföljebb öt más egyénen keresztül, kik közül az egyik neki személyes ismerőse, kapcsolatot tud létesíteni az illetővel, csupa közvetlen - ismeretség alapon…” Lehet, hogy az író ezt csak tréfának vagy fikciónak szánta, de viszonylag közel lőtte be a számot. Stanley Milgram kutatásai alapján arra jutott (1967), hogy a társadalmi hálókban az átlagos távolság, (azaz, hogy egy véletlenszerűen kiválasztott ember egy másik véletlenszerűen kiválasztott embertől hány ismerősön keresztül érhető el) legfeljebb 6 „ismerősnyire” van.
Az Erdő-Rényi modell nagy kérdése, hogy érdemes-e hinni abban, hogy minden hálózat véletlenszerű? Például az emberen belüli kémiai anyagok véletlenszerűen kapcsolódnak össze? Hol van a funkcionalitás és a hatékonyság? Biztos, hogy a véletlenszerű a legjobb? Lehet, hogy a statisztikában igen (elméletileg), de mégsem azt használjuk mintavételre, mert nem hatékony, drága, nehezen megvalósítható. Ugyanez a helyzet az Internettel és midenféle hálókkal, logikusan kell, hogy felépüljenek, hiszen így tudnak a leghatékonyabban működni. Ebből adódik a kérdés, hogy minden kapcsolatnak és csomópontnak ugyanolyan fontosságot kell tulajdonítani? Másik nagy kérdése a komplex hálózatok vizsgálatának a gráfelmélettel szemben, hogy a hálózatok növekednek, így a fokszámok változnak, hogyan hat ez a véletlen hálózatok paradigmájára? Gondoljunk csak az Internetre mint komplex hálózatra, folyamatosan növekszik, változik; új oldalak jelennek meg mások eltűnnek. De, hogy kézzelfoghatóbb példával éljek; ismerőseink és főleg közeli barátaink száma is folyamatosan változik, új ismerettségeket kötünk, másoktól teljesen eltávolodunk, esteleg valaki meghal.
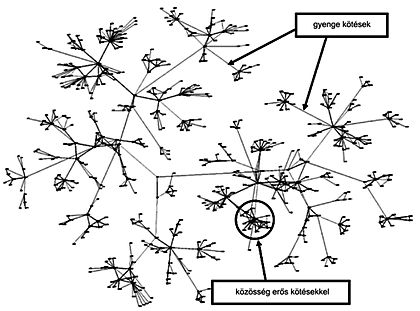A kötések erősségét már régóta megkülönböztették a kutatók (gyenge, erős), persze sokszor nehezen kvantifikálhatóak a különbségek (főleg társadalmi hálóknál). A „kisvilág” modellre reflektálva Mark Granovetter szerint a gyenge kötések tartják egyben a társadalmat és a véletlen gráfok modellje itt már nem állja meg a helyét. Hiszen, ha mindekinek közel azonos számú ismerőse lenne, ugyanolyan erősségű kapcsolatokkal, akkor megkérdőjeleződne a fent olyan szépen bemutatott kisvilág modell. Így nem lehetne Barack Obama anyukám nővérének a munkatársának a férjének a főnökének a volt egyetemi csoporttársának az ismerőse. Hiszen ezek a kapcsolatok nem ugyanolyan erősségűek. Bebizonyításra került, hogy az információáramláshoz inkább a gyengekötések szükségesek, mint a közeliek, hiszen a kis közösségekben bent ragad az információ és az újítások nehezebben jelennek meg. (Ezt a tulajdonságát használjuk ki a kapcsolati hálóknak ternékterjesztési stratégia kidolgozásánál is.) Tehát a gyenge kapcsolatok összezsugorítják a világot, az erős kapcsolatok pedig stabiilizálják (NPS-nél lényegében ezt vizsgáljuk).
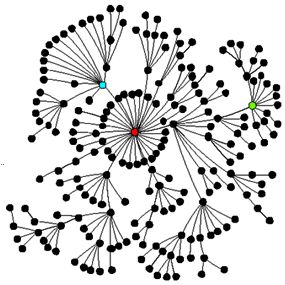Az ezredfordulón érkezett meg a hálózatkutatás és a marketing egyesülésének lehetősége a skálafüggetlen hálózatokkal. Barabási Albert-László és kutatócsoportja arra lett figyelmes az Internet vizsgálata közben, hogy léteznek nagyobb csomópontok. Tehát nem minden ponthoz csatlakozik be ugyanannyi él, a felépítés nagyon hierarchikus és az egyes hálózati aktorok nem egyformán fontosak. (Barabási nagysikerű Behálózva című könyve lényegében erről szól, számos érdekes példán bemutatva a felfedezés nagyszerűségét. ) Vannak központi szereplők, akiknek sokkal több kapcsolatuk van, ilyen például internetes portáloknál a Google, de embereknél is megtalálható ez a személy. És nekünk ők kellenek, illetve nekik egyes típusaik…
A következő részben részletesen leírom, hogy pontosan mik is azok a skálafüggetlen hálózatok és miért is volt ez akkora újítás (főleg nekünk, piackutatóknak)!
Források:
• Barabási Albert-László: Behálózva – a hálózatok új tudománya, Magyar Könyvklub, 2003
• Barabási Albert-László: A hálózatok tudománya: a társadalomtól a webig, Magyar Tudomány 2006/11
• Kertész János : Súlyozott hálózatok:A tőzsdétől a mobiltelefóniáig in Magyar Tudomány, 2006/11 1313. o http://www.matud.iif.hu/06nov/05.html (2010-11-15)
• Tóth Zsolt: Tudáshálók a gazdasági felsőoktatásban (PhD értekezés) 2009, Sopron
Ki vagyok én?
Vásárhelyi Orsolya vagyok az ELTE Társadalomtudományi Karán, Survey Statisztika mesterképzésén, első éves hallgató. Jelenleg a Maven7 Hálózatkutató cég gyakornokaként tevékenykedem. Remélem érdekeségekkel, újdonságokkal szolgálnak a cikkek és másokra is átragaszthatom hálózatos mániámat. (Hiszen a kedvelés is hálózatos úton terjed!)
