Folytatjuk a hálózatokról, hálózatkutatásról indított sorozatunkat. Vendégszerzőnk, Vásárhelyi Orsolya, az előző részben az alapokat mutatta be, most pedig megismertet bennünket a skálafüggetlen hálózatokkal.
Eljött az idő, hogy továbbhaladjunk a hálózatkutatás történetében és megérkezzünk napjainkhoz. Az előző részt a ma már Barabasilabnak (http://www.barabasilab.com/) nevezett kutató csoport felfedezésével fejeztük be. A skálafüggetlenség fogalmát nem Barabásiék kutatócsoportja alkotta meg, de az ő felfedezésük tette ismertebbé és gyakorlatban használhatóvá az elméletet.
Tehát, mik is ezek a skálafüggetlen hálózatok? Matematikailag akkor nevezünk egy hálózatot skálafüggetlennek, ha a fokszám eloszlása hatványfüggvényt követ. Magyarul - megfigyelhetőek csomópontok, melyeknek kiemelkedően magas a fokszáma (sok él fut be ide) és ezek a csúcsok általában össze vannak kötve egymással.[1] Az előzőekben már utaltam a Normális eloszlásra, mely a Gauss-féle haranggörbével jellemezhető. A skálafüggetlenség vizsgálatáig a tudósok, úgy gondolták, hogy a természetben ez a fajta eloszlás a leggyakoribb, ezért is lett a neve „normális”. Ilyen például az emberi testmagasság, ami egy átlagos értékkel leírható és e körül szóródnak az adatok. A hatványfüggvénynél azonban az átlag semmiképpen sem a legjobb mérőszám. Az alábbi kép jól megragadja a két eloszlás különbségét.
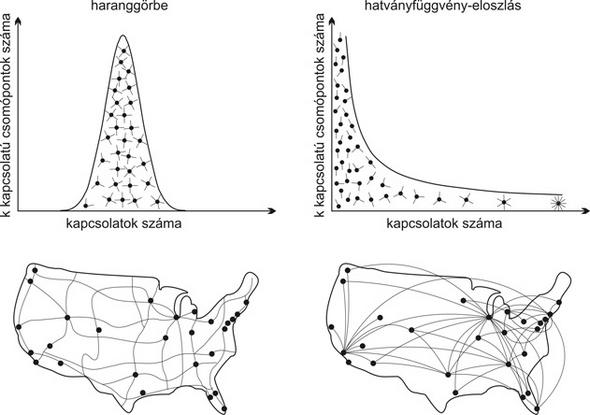 [2]
[2]
A bal oldali kép az USA főbb autópályáit mutatja, melyeknek eloszlása normális. Az autóút-hálózat tervezésénél a cél, hogy az ország egységesen legyen lefedve, tehát elméletileg létezik egy átlagos lefedettséget mutató szám. A jobb oldali ábra pedig a fontosabb repülési útvonalak hálózatát mutatja, mely hatvány eloszlású. Látszik, hogy nem egyenletes a lefedettség, a Keleti part metropoliszai fontosabb csomópontok, több él csatlakozik ide, mint például az ország közepén lévő városokba. Képzeljük el, hogy egy amerikai város szeretne egy repteret. Felépítik és azon kezdenek el morfondírozni, hogy merrefelé indítsanak járatokat? A válasz egyértelmű - a különböző metropoliszokat (nagyobb csomópontokat) kell megcélozni, ahonnan sokfelé tovább lehet utazni. Ezt a jelenséget nevezzük preferenciális kapcsolódásnak. Ezt fedezte fel Barabási Albert-László és kolléganője Albert Réka 1999-ben, az Internet szerkezetének vizsgálata közben. (Az így kialakuló hálók a skálafüggetlen hálózatoknak persze csak egy típusát adják, de ez segít a fogalom megértésében.)
A skálafüggetlen hálózatok rendelkeznek a small-world effektussal, azaz a kevesebb kapcsolattal rendelkező csomópontok sűrű részhálókat alkotnak és ezeket a részhálókat a nagy fokszámú csomópontok kötik össze. Ezek a hálók hibatűrők, ha bizonyos nem kiemelkedő elemeiket eltűntetjük a hálózat fennmarad, azonban, ha egy csomópont esik ki kis darabokra esik szét az egész gráf. Ilyen csomópont például New York az amerikai légi közlekedés hálózatában, a Google a világhálóban vagy csak a magyar oldalakat tekintve jó példa az Index és az Origo.
A hagyományosan értelmezett marketingben és piackutatásban nyilvánvalóan a pontok alatt fogyasztókat, azaz embereket értünk. (Persze fontos kérdés a médiahálózatok elemzése vagy a termékpreferenciáké is.) Kapcsolati hálónkra egyértelműen igazak a fentebb említettek. Gondoljunk csak bele; vannak olyan ismerőseink, akik szinte „mindenkit” ismernek és mindenki tudja a nevüket, de nem feltétlenül népszerűek a szó hagyományos értelmében. Az ilyen embereke szoktuk mondani, hogy érdemes jóban lenni velük vagy, hogy az ilyen kapcsolatok aranyat érnek. És ez így is van.
A hálózatkutatás módszereivel ki lehet mutatni – a marketingben gyakran meghatározó személynek vagy véleményformálónak nevezett, olyan egyéneket, akik az adott termékről többet beszélnek, mint egy átlagos ember. Jellemző rájuk, hogy sok ismeretségi kapcsolatuk miatt az elsők között vannak, akik egy új termék bevezetését észlelik és elkezdik használni. Önmagukban még nem feltétlenül újítók, azonban a leggyorsabb adaptálóknak tekinthetőek. Az új termék részükről való elfogadása kulcsfontosságú, ha a középpont elutasít egy innovációt, olyan áthatolhatatlan és befolyásos fal képződik, hogy az újítás biztosan megbukik, ha azonban elfogadja nagyon sok emberre hat a döntése – a termék sikeressége predesztinálva lesz. [3]
“Ilyen statisztika, mellyel kimutatható például egy véleményvezér a csomósodási együttható (clustering coefficient), vagy a motívumok statisztikája. A csomósodási együttható egy csúcson azt méri, hogy figyelembe véve a szomszédok adott számát, az elvileg lehetséges háromszögek hányad része valósul meg a hálózatban. Ez a szám, amely 0 és 1 között változhat, azt mutatja, hogy mennyire hajlamosak a „barátok egymással barátkozni”. A motívumstatisztika egy (véletlen) referenciamodellhez viszonyítva jelzi, hogy egy adott topológiájú részgráf szignifikánsan gyakori-e a vizsgált hálózatban. Ha igen, akkor feltehető, hogy a részgráfnak fontos szerepe van a működésben.” [4]
Szociológusok és marketingszakértők tökéletesen tudatában vannak ezeknek a jelenségeknek. De egészen a 2000-es évekig a középpontokat egyedülálló jelenségeknek tekintették, nem nagyon tudták, miért és mennyi létezik belőlük. A szociális hálózatmodellek nem támogatták a középpontok létezését. A skálafüggetlen hálózatok által nyújtott szerkezet első ízben biztosította a középpontok megérdemelt szerepét. [5]
Hálózati és marketing szempontok alapján a fogyasztók három típusát különböztethetjük meg; a már említett véleményvezéreket ( Opinion Leaders), az információ-elosztókat (Hubs) és a követőket. A véleményvezér és az információ-elosztó személye akár egybe is eshet, hiszen az egyik inkább egy attitűd a másik pedig a hálózatban elfoglalt pozícióval összefüggő tulajdonság. Egy marketing stratégia megtervezésénél különösen fontos ezen szereplők különböző igényeit felmérni és rajtuk keresztül kutatni a piacot. Ha sikerül megnyernem a véleményvezért, a hub-bal elhinteni az információt és tesztelni a követők hozzáállását máris a kezünkben van a tökéletes termékterjesztési terv. Ez persze korántsem egyszerű és nem minden kampánynál alkalmazható, rengeteg múlik a rendelkezésre álló adatok mennyiségén és minőségén.
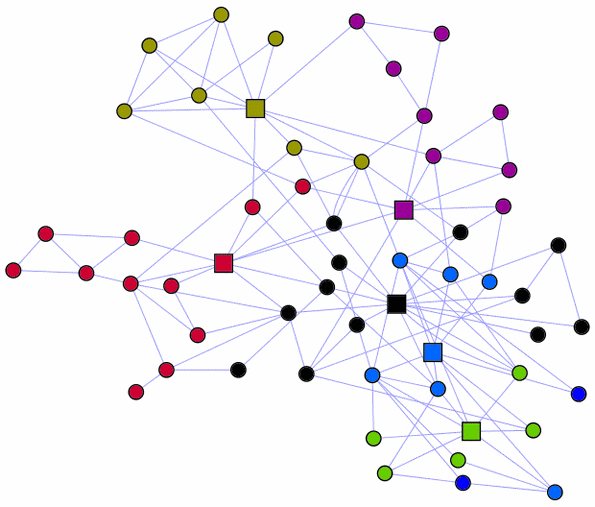
Kép: A négyzetek mutatják a véleményvezéreket, melyek közül a bordó és a keki információ-elosztó szerepet is betölt. A színek különböző clusterekre utalnak.[6]
A következő részben egy konkrét piackutatási problémán mutatom be az alkalmazási módszereket és lehetőségeket.
Hogy senki ne maradjon hálózatok nélkül a következő cikkig:
Blog: Hetent frissülő a hálózatokhoz, hálózatkutatáshoz kapcsolódó információk, tanulmányok (http://network.blog.hu/)
Konferncia: Circuits of profit- Üzletihálózatkutatás konferencia (http://circuitsofprofit.com/)
Könyvek:
Barabási Albert-László: Behálózva (http://www.libri.hu/konyv/behalozva.html)
Barabási Labert-László: Villanások (http://www.libri.hu/konyv/villanasok-1.html)
Hálózatkutató cég: Maven7 (http://www.maven7.hu/index_hu.php)
Hivatkozások:
[1] http://en.wikipedia.org/wiki/Scale-free_network (2011-03-14)
[2] Barabási Albert-László: Behálózva – a hálózatok új tudománya, Magyar Könyvklub, 2003
[3] http://www.maven7.hu/index_hu.php?page=uzleti_halozatok (2011-03-14)
[4] Kertész János : Súlyozott hálózatok:A tőzsdétől a mobiltelefóniáig in Magyar Tudomány, 2006/11 1313. o http://www.matud.iif.hu/06nov/05.html (2010-13-14)
[5] Részlet az Országos Piackutató Verseny győztes HÁLÓWIN csapatának írásbeli anyagából
[6] Részlet az Országos Piackutató Verseny győztes HÁLÓWIN csapatának szóbeli prezentációjából
Ki vagyok én?
Vásárhelyi Orsolya vagyok az ELTE Társadalomtudományi Karán, Survey Statisztika mesterképzésén, első éves hallgató. Jelenleg a Maven7 Hálózatkutató cég gyakornokaként tevékenykedem. Remélem érdekeségekkel, újdonságokkal szolgálnak a cikkek és másokra is átragaszthatom hálózatos mániámat. (Hiszen a kedvelés is hálózatos úton terjed!)







